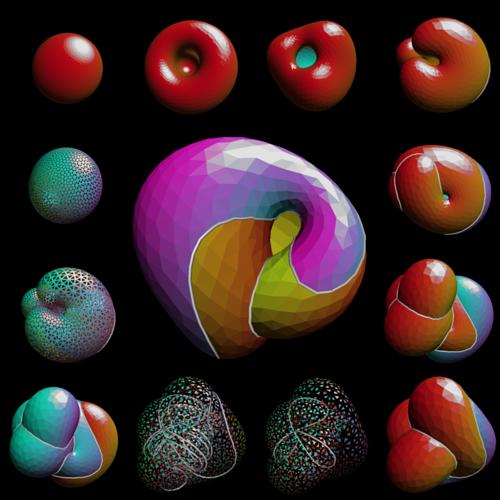
Figure 10:
This three-fold minimax eversion starts (top row, clockwise)
with a gastrula stage like that of the two-fold eversion, but
the three-fold symmetry means that three fingers reach up from the neck
instead of two. They intersect each other (righthand images)
and then twist around, while complicated things are happening inside.
The lower right and central images are near the halfway model.
The two images at the bottom with gaps between the triangles
show the double-curves; the Boy's surface halfway-model intersects itself in a
"propeller" curve, which then gets replaced by its four-fold cover
as we separate the two sheets.
Acknowledgments
The minimax sphere eversions described here are work
done jointly in collaboration with
Rob Kusner, Ken Brakke, George Francis, and Stuart Levy,
to whom I owe a great debt.
I would also like to thank Francis, Robert Grzeszczuk,
John Hughes, AK Peters, Nelson Max and Tony Phillips
for permission to reproduce figures from earlier sphere eversions.
This paper first appeared in the proceedings of
two summer 1999 conferences on Mathematics and Art:
ISAMA 99 (June, San Sebastián, Spain),
and Bridges (July, Kansas).
I wish to thank Nat Friedman, Reza Sarhangi, and Carlo
Séquin for the invitations to speak at these conferences.
I thank Slavik Jablan for formatting
this online web version of the paper.
My research is supported in part by NSF grant DMS-97-27859.

REFERENCES