|
Our minimax sphere eversions differ from the earlier ones mentioned above in that they are computed automatically by a process of energy minimization. The elastic bending energy for a stiff wire is the integral of squared curvature. For a surface in space, at each point there are two principal curvatures, and their average, the mean curvature, shows how much the surface deviates from being minimal. The integral of squared mean curvature is thus a bending energy for surfaces, often called the Willmore energy [Wi]. (Gauss-Bonnet shows this is mathematically equivalent to many other formulations.) |
|
Among all closed surfaces, the round sphere minimizes this bending energy. (The energy is scale-invariant, and we normalize so the sphere has energy 1.) It is also known [LY,Ku] that any self-intersecting surface with a k-tuple point has energy at least k. To evert a sphere, it is necessary to pass through some stage with a quadruple point [BM,Hu], and hence energy at least 4. |

|
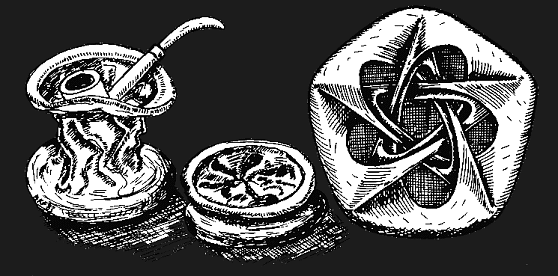
Figure 5: These sketches by George Francis show a French tobacco pouch, and a cutaway view of the halfway-model for the order-five tobacco-pouch eversion. |
|
Francis and Morin realized that the Morin surface and Boy's surface are just the first in an infinite sequence of possible halfway-models for what they call the tobacco-pouch eversions (see Fig. 5, taken from [Fr]). In the 1980s, Robert Bryant [Bry] classified all critical points for the Willmore energy among spheres; they all have integer energy values which (except for the round sphere) are at least 4. Rob Kusner, being familiar with both of these results, realized that he could find, among Bryant's critical spheres, ones with the tobacco-pouch symmetries. Among surfaces with those symmetries, Kusner's have the least possible Willmore energy. |
|
In particular, Kusner's Morin surface with four-fold orientation-reversing symmetry has energy exactly 4. If we don't enforce this symmetry, then presumably this surface is an unstable critical point: a saddle point for the energy. Pushing off from this saddle in one downhill direction, and flowing down by gradient descent, we should arrive at the round sphere, since it is the only critical point with lower energy. (Of course, there's not enough theory for fourth-order partial differential equations for us to know in advance that the surface will remain smooth and not pinch off somewhere.) |
|
As we saw before, such a homotopy, when repeated with a twist, will give us a sphere eversion. This eversion starts at the round sphere (which minimizes energy) and goes up over the lowest energy saddle point; then it comes back down on the other side arriving at the inside-out round sphere. |
|
Around 1995, in collaboration with Kusner and Francis, I computed this minimax eversion [FSK] using Ken Brakke's Evolver [Bra], which is a software package designed for solving variational problems, like finding the shape of soap films or (see [HKS]) minimizing Willmore energy. We were pleased that the computed eversion was not only geometrically optimal in the sense of requiring the least bending, but also topologically optimal, in that it was one of the Morin eversions with the fewest topological events. |
|
Computations of the higher-order minimax sphere eversions [FSH] (like the one with a Boy's surface halfway-model) had to wait until Brakke and I implemented some new symmetry features in the Evolver (see [BS]). A minimax tobacco-pouch eversion, whose halfway-model has 2k-fold symmetry, will break some of this symmetry. But it will maintain k-fold symmetry throughout, and the Evolver now works with only a single fundamental domain for this symmetry. We can find the initial halfway-models by minimizing bending energy while enforcing the full symmetries. |
|
Alternatively, we can compute them directly. Bryant's classification says that all critical spheres are obtained as conformal transformations of minimal surfaces, and Kusner gave explicit Weierstrass parameterizations for the minimal surfaces he needed. In Fig. 6 we see the minimal surface with four flat ends which transforms into our Morin halfway-model. |
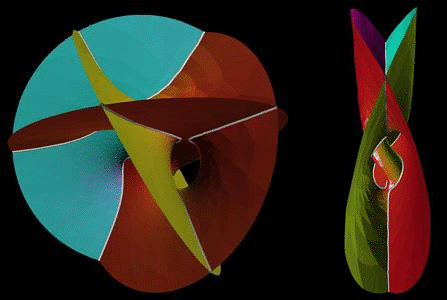
|
Figure 6: This minimal surface (left), with four flat ends, gives rise to Kusner's Morin surface of least Willmore bending energy, when a conformal Möbius transformation is applied to compactify it. If the transformation sends the double-tangent point to infinity, we get an interesting picture (right). |
|
The Evolver works with triangulated approximations (with a few thousand triangles) to the true smooth surfaces, and we update the triangulation as needed to maintain a good approximation. Initially, it's necessary to use the second-order Hessian methods implemented in the Evolver to push off the saddle point and find our way downhill. |
|
In 1998, working with Francis and Stuart Levy, I produced a computer graphics video, "The Optiverse" [SFL], which shows the first four minimax eversions. It premiered at the International Congress of Mathematicians in Berlin, and was also shown at SIGGRAPH and written up nicely in Science News [Pe]. (The video was produced at the NCSA at the University of Illinois. More information about it is available on our website at http://new.math.uiuc.edu/optiverse/.) |
|
Many scenes in the video (as in Fig. 7) capture views of the eversion also available in our real-time interactive computer animation running on desktop workstations or immersive virtual-reality environments. These show a solid, colored surface, with white tubes around the double-curves of self-intersection. Here we are aware of the triangulation used for the computation, especially if we leave gaps between triangles or in their middles. |
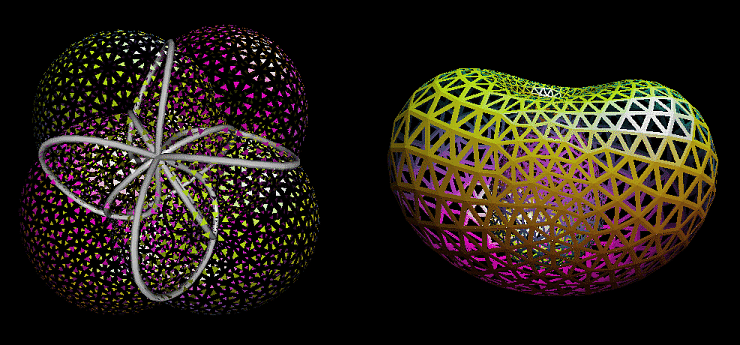
|
Figure 7: The Morin halfway model (left), shown with all triangles shrunk, has an elaborate set of double curves where the surface crosses itself. A late stage in the eversion is like a gastrula (right), shown here as a triangular framework. |
|
But no one method of rendering can give all useful visual information
for a nonintuitive phenomenon like a self-intersecting surface.
So other parts of the video (like Fig. 8)
were rendered as transparent soap films,
with the soap bubble shader I wrote for Renderman (see [AS].

NEXT |