| Why Symmetry? Why Asymmetry? by Michael Leyton, Page 3. To go back to: Page 2
Corroborating Examples To see that our two rules consistently yield satisfying process-explanations, let us obtain the processes that these rules give for a large set of shapes. We shall take the set of all possible shapes that have 8 extrema or less. Such shapes fall into three levels: shapes with 4 extrema, shapes with 6 extrema, and shapes with 8 extrema. The reason is that, there cannot be shapes with an odd number of extrema - because maxima have to alternate with minima of curvature - and there cannot be shapes with less than 4 extrema by a theorem in differential geometry. We will refer to the three successive levels of shapes as Levels 1, 2, and 3 respectively. There are a total of 21 shapes, of succesively increasing complexity. Since it takes a while for the internet to mount these shapes, lets make our comments first: (1) When the shapes appear, the reader will notice that, on each shape, each extremum is marked by one of four symbols: M+, M-, m+, m-. This is because there are mathematically four kinds of curvature extrema: Positive Maxima (M+); Negative Maxima (M-), Positive minima (m+); and Negative minima (m-). (2) When one surveys the shapes, one finds that there is the following simple rule that relates the type of extremum to an English word for a process: SEMANTIC INTERPRETATION RULE M+ is always a protrusion
Remember, as you look at the figures, the process arrows are inferred by the two simple rules we gave above: The Symmetry-Curuvature Duality Theorem, and the Interaction Principle.
The 21 shapes:
Shapes with 4 extrema: 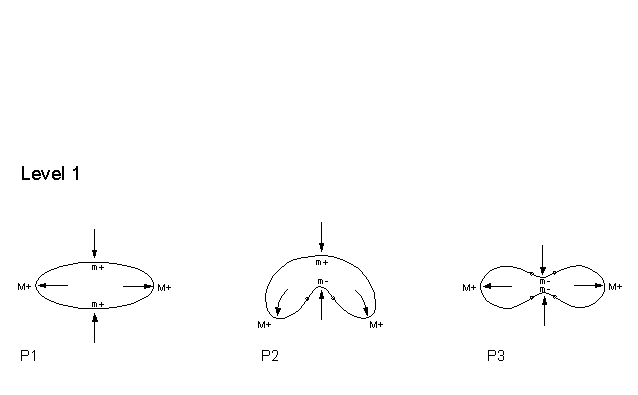
Shapes with 6 extrema: 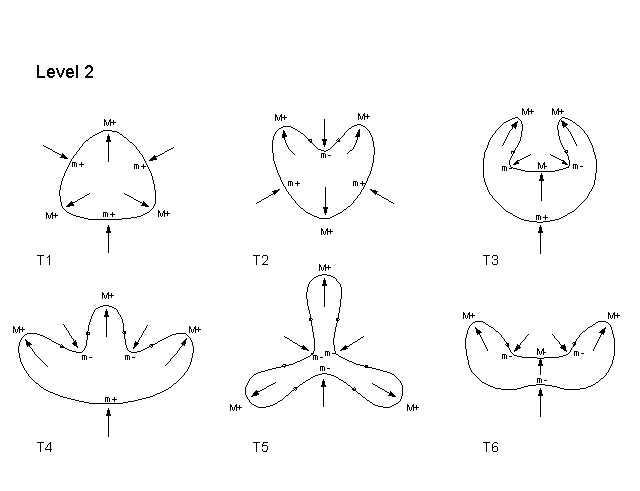 Shapes with 8 extrema: Set 1:  Set 2: 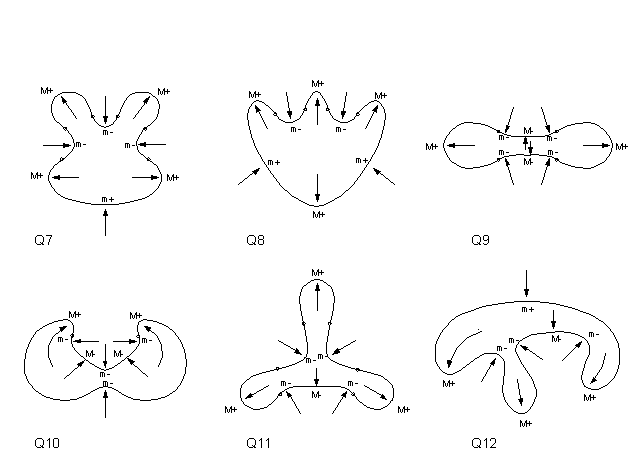 Let us now go more deeply into the structure of these histories. To continue: NEXT PAGE
|